 CGENN layers
CGENN layersAbstract
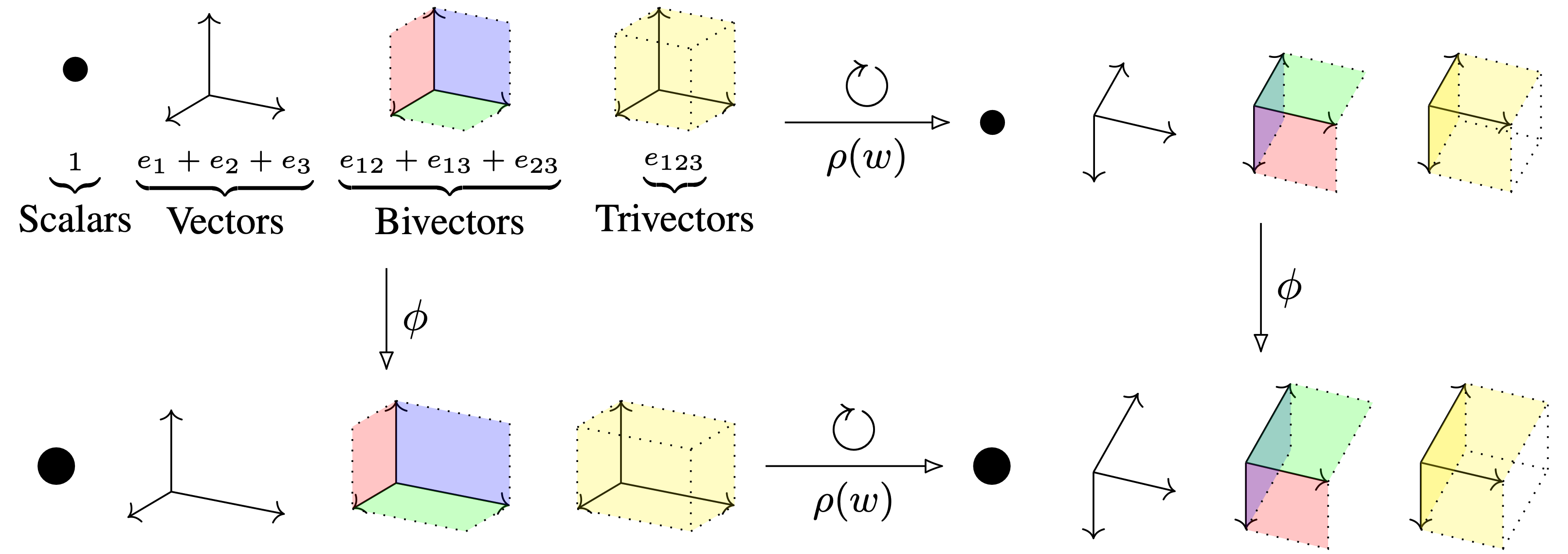
We introduce Clifford Group Equivariant Neural Networks: a novel approach for constructing O(n)- and E(n)-equivariant models. We identify and study the Clifford group, a subgroup inside the Clifford algebra tailored to achieve several favorable properties. Primarily, the action of the group forms an orthogonal automorphism that extends beyond the typical vector space to the entire Clifford algebra while respecting the multivector grading. This leads to several non-equivalent subrepresentations corresponding to the multivector decomposition. Furthermore, we prove that the action respects not just the vector space structure of the Clifford algebra but also its multiplicative structure, i.e., the geometric product. These findings imply that every polynomial in multivectors, An advantage worth mentioning is that we obtain expressive layers that can elegantly generalize to inner-product spaces of any dimension. We demonstrate, notably from a single core implementation, state-of-the-art performance on several distinct tasks, including a three-dimensional n-body experiment, a four-dimensional Lorentz-equivariant high-energy physics experiment, and a five-dimensional convex hull experiment.